Wetenschapper lost 2.000 jaar oud aberratieprobleem op

Het ontstaan van het aberratieprobleem
De eerste die dit aberratieprobleem formuleerde was de Griekse wiskundige Diocles. Hij gaf aan dat lenzen gemaakt zijn van sferische oppervlakken en het probleem wat hierdoor ontstaat als er lichtstralen buiten het midden van de lens niet kunnen worden scherp gesteld op de gewenste afstand in één punt, vanwege het verschil in lichtbreking. Hierna zijn zowel Isaac Newton, Gottfried Leibniz en René Descartes met het probleem aan de slag gegaan, zonder succes.

Lees ook: Onderzoek: fotografen worden uitgebuit omdat ze van hun werk houden
Later formuleerden Wasserman en Wolf het aberratieprobleem en stelden voor twee asferische aangrenzende oppervlakken te gebruiken om sferische en coma-aberraties te verminderen. Deze asferische elementen waren echter een stuk duurder, doordat deze moeilijker op een precieze manier te vervaardigen zijn. Het probleem loste het grotendeels op, toch bleef hier de vervaardiging van de asferische elementen belangrijk en werd het probleem niet 100% opgelost.
Oplossing aberratieprobleem
Recentelijk zijn wetenschapper Héctor A. Chaparro-Romo, promovendus aan de Nationale Autonome Universiteit van Mexico en Rafael González, doctoraalstudent uit Tec de Monterrey met het aberratieprobleem van lenzen aan de slag gegaan en hebben een oplossing gevonden. Ze ontwikkelden een formule waarmee er een lens met een vrije vorm gecreëerd kan worden, die ervoor zorgt dat de lichtstralen de vervolglens evenredig bereiken. Het weergegeven beeld is voor 99.9999999999% vrij van aberraties.

Lees ook: Model Gigi Hadid claimt auteursrecht vanwege lachen op foto
De onderstaande afbeelding toont de algebraïsche formule. 'In deze vergelijking beschrijven we hoe de vorm van het tweede asferische oppervlak van de gegeven lens een eerste oppervlak moet krijgen,' legt González uit. "Het tweede oppervlak is zodanig dat alle aberratie die door het eerste oppervlak wordt gegenereerd, wordt gecorrigeerd en de sferische aberratie wordt geëlimineerd."
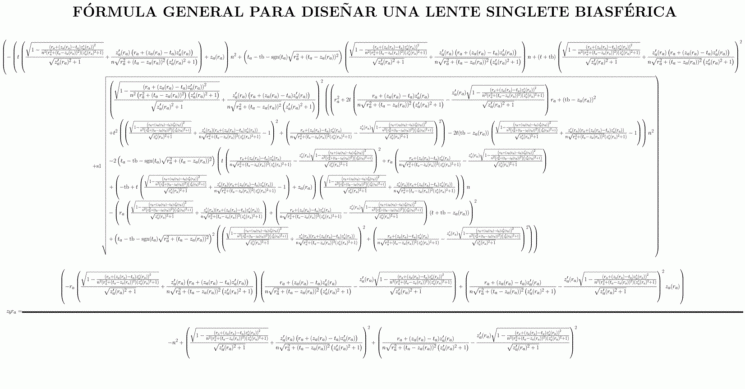
De oplossing is niet alleen bruikbaar in de fotografie. Microscopen, telescopen... Er zijn een hoop andere, al dan niet wetenschappelijke, toepassingen die de formule biedt. Als deze techniek wordt toegepast in de fotografie zal dit leiden tot een stuk scherpere beelden.
Lees hier en hier meer over het onderzoek door te drukken op 'get pdf.'






